Lekcja gry: "Formuły zredukowanego mnożenia"

Cele:
Edukacja:

• Podsumowanie i usystematyzowanie wiedzy studentów na ten temat.
• Rozwijanie umiejętności korzystania z zredukowanych formuł mnożenia przy rozwiązywaniu zadań.
• Przygotować się do kontroli.

Opracowanie:

1. Rozwijanie zainteresowania poznawczego i poszerzanie horyzontów studentów.
2. Naucz się stosować wiedzę w praktyce.

Edukacja:

1. Uczenie studentów umiejętności i umiejętności w zespole.

Rodzaj lekcji: uogólniona lekcja powtarzania.

Wyposażenie: instalacja multimedialna.

Postęp klas

Slide 1-2.

1. Moment organizacyjny

3.

Algebra jest tylko matematycznym językiem przystosowanym do określenia relacji pomiędzy ilościami.
And. newton

Slide 4.

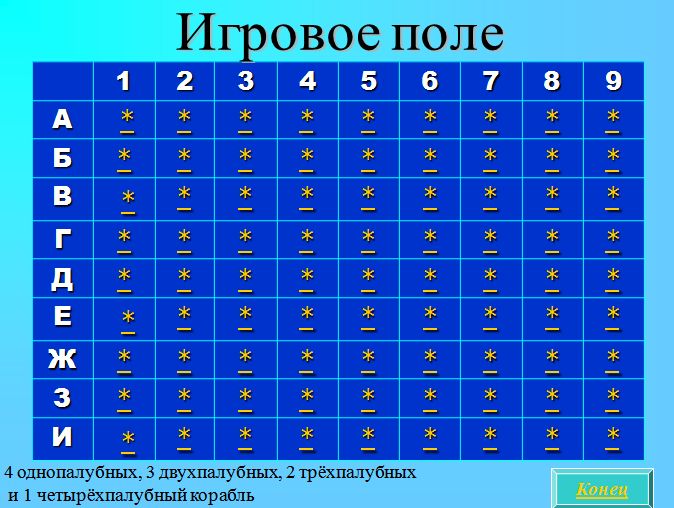
2. Zasady gry "Matematyczna bitwa morska".

• Do gry, klasa jest podzielona na 2 grupy. Zespoły na przemian strzelać do statków, nazywając komórki pola gry (zjeżdżalnia 5). Poprzez naciśnięcie symbolu * w określonej komórce sprawdza się skuteczność ruchu.
• Jeśli jedna z drużyn popełniła błąd, ruch przechodzi (zjeżdżalnia 6), jeśli historyczne odniesienie wypadnie, po zapoznaniu się z nim, zespół ma prawo do innego ruchu, jeśli wszystkie zespoły zostaną trafione, zadanie jest oferowane. Priorytetowe prawo do odpowiedzi jest przyznawane zespołowi, który wykonał udany ruch. Jeśli ten zespół popełni błąd, przeciwnicy odpowiedzą. Punkty przyznawane są zespołowi, który udzielił prawidłowej odpowiedzi.
• Czas na wykonanie zadania jest ograniczony. Po przydzielonym czasie sprawdzamy odpowiedź. Kliknięcie na słowo "punkty" idziemy do tabeli wyników (zjeżdżalnia 25) i wprowadzić punkty do zespołu, który poprawnie ukończył zadanie. Następnie, klikając na słowo "back" ponownie powrócić do pola gry (slajdów 5).

Zjeżdżalnia 5.

3. Przesyłki do realizacji

Pytania o pracę ustną.
Zjeżdżalnia 7.
A-1. Jaka jest różnica między tymi wyrażeniami? (2 punkty)
8.
A- 5. Jaki jest kwadrat sumy i kwadrat różnicy dwóch wyrażeń? (2 punkty)
Zjeżdżalnia 9.
A- 6. Jaka jest suma kostek i różnica kostek dwóch wyrażeń? (2 punkty)
Slide 10.
A- 7. Jaki jest kwadrat sumy trzech wyrażeń? (2 punkty)
Slide 11.
A- 9. Czym jest sześcian różnicy i sześcian sumy dwóch wyrażeń? (2 punkty)

Zadania do wykonania w notesie.

Slide 12.
B-1. Wyobraź sobie wyrażenie wielomianowe (2m + 5) (5- 2m + 4m)²(4 punkty).
Odpowiedź: 25
Slide 13.
B3. Wyobraź sobie wyrażenie wielomianowe (2x + 3)²- 4x2 (4 punkty).
Odpowiedź: 12x + 9
Slide 14.

B- 4. Wyobraź sobie wyrażenie wielomianowe (2x-3u)²+ (3x + 2u)²(4 punkty).
Odpowiedź: 13x²+ 13²
Slide 15.

B-5. Wyobraź sobie wyrażenie wielomianowe (2x-3) (2x + 3) - (2x-1)²(4 punkty).
Odpowiedź: 4x- 10
Slide 16.

B-6. Wyobraź sobie wyrażenie wielomianowe (2x + y)³-6hu (2x + y) (4 punkty).
Odpowiedź: 8x³+³
Zjeżdżalnia 17.

B-9. Pomyśl o wyrażeniu wielomianowym (m- n)³+ 3mn (m- n) (4 punkty).
Odpowiedź: m³+ n³
Zjeżdżalnia 18.

D- 8. Pomnóż wielomian (2x + 1)²- 16 (6 punktów).
Odpowiedź: (2x-3) (2x + 5).

Slide 19.
E- 2. Pomnóż wielomian (x -2)²- (x + 1)²(6 punktów).
Odpowiedź: -3 (2x-1)

Slide 20.
G- 4. Wyobraźcie sobie w formie pracy x6 -27 (8 punktów).
Odpowiedź: (x)²-)⁴+ 3x²+ 9)

Slide 21.
G- 5. Przelicz na wielomian (3x + y2)³(8 punktów).
Odpowiedź: 27x³+ 27x²у²+ 9ha⁴+ u6

Slide 22.
G-7. Rozwiąż równanie: 4x2 + 4x + 1 = 0 (10 punktów).
Decyzja
4x²+ 4x + 1 = 0
(2x + 1)²= 0;
2x + 1 = 0;
2x = -1;
x = 1: 2;
x = 0,5.
4 · 0, 5²+ 4 · 0,5 + 1 = 0.
0 = 0
Odpowiedź: 0.5
Slide 23.
G- 8. Rozwiąż równanie: (7x)²- (x- 8) (x + 8) = 43 (10 punktów).
Rozwiązanie.
(7x)²- (x- 8) (x + 8) = 43;
72-2 · 7 · x + x²- (x2- 82) = 43;
49- 14x + x²-²+ 44 = 43;
-14x = -70;
x = -70: 14;
x = 5.
(7- 5)²- (5- 8) (5 + 8) = 43
43 = 43.
Odpowiedź: 5
Slide 24.
E- 2. Znajdź najniższą wartość trójczłonowego kwadratu x2 + 2 x + 7 (12 punktów).
Rozwiązanie.
x2 + 2 x + 7 = (x)²+ 2 · 1 · x + 12- 12 + 7 = (x + 1)²+ 6
Ten trzeci termin zakłada najniższą wartość, gdy (x + 1) 2 przyjmuje najniższą wartość, tj. (x + 1)²= 0.
Dlatego najmniejsza wartość trzech wyrażeń kwadratowych to 6.
Odpowiedź: 6
Slide 25.
E- 3. Przy jakiej wartości x z dowolnej wartości x kwadrat trzy wyrazy x²-12x + 50 jest najmniej ważne? (12 punktów).
Rozwiązanie.
х²-12x + 50 = x²-2 · 6 · x + 36- 36 + 50 = (x- 6)²+ 14
Ta triada jest najmniej ważna, gdy
(x- 6)²= 0;
x- 6 = 0;
x = 6.
Odpowiedź: 6
Slide 26.
Nagroda E- 4. (6 punktów).

4. Tło historyczne
Ponieważ formuły skróconego mnożenia są badane w klasie algebry, te historyczne odniesienia pozwolą Ci dowiedzieć się, skąd pochodzi ta nazwa i którzy naukowcy wnieśli wielki wkład w rozwój tej nauki.
Slide 27.

• Słowo "Algebra" powstało po pojawieniu się traktatu matematycznego i astronoma Mohammeda ben Musa al- Khwarizmi (787- ok. 850). Termin al- Jabr, zaczerpnięty z tytułu tej książki, został później użyty jako algebra.

Zjeżdżalnia 28.

• Muhammad Al- Khwarizmi (787- około 850) napisał podstawowe traktaty o arytmetyce i algebrze.

Slide 29.

• Diophantus Alexandrovsky (III wiek). W jego książce "Arytmetyczne" znajdują się rudymenty symbolizmu liter i specjalne notacje dla stopni, a także znak równości, krótki zapis zasad mnożenia, problemy prowadzące do złożonych systemów równań algebraicznych.

Zjeżdżalnia 30.

• François Viet (1540- 1603) wprowadził symbole algebraiczne, zaczął oznaczać liczby liter, rozwinęła podstawy algebry.

Slide 31.

• Pierre Fermat (1601- 1665) był zaangażowany w teorię rozwiązywania równań algebraicznych przy pomocy kilku zmiennych.

Slide 32.

• René Descartes (1596- 1650) rozszerzył zapas liczb, z którymi można wykonać działania. Wprowadzone: x, y, z - zmienne, niewiadome; a, b, c - stałe, parametry; znak podziału.

Slide 33.

• Gottfried Wilhelm Leibniz (1446- 1716) stworzył podstawy analizy matematycznej, wprowadził wiele koncepcji i symboli.

Slide 34.
5. Wynik lekcji. Liczenie punktów i przyznawanie zwycięskiej drużyny.

Zjeżdżalnia 35.
Sprawdzam położenie statków.

6. Praca domowa.

{moduł Google _ kvadrat}

Prezentacja w formacie .ppt i podsumowanie lekcji w formacie .doc 2.54 Mb